Drehkörper - Volumen- und Mantelflächenberechnungen |
Baustein 2 - 1(3) |
|
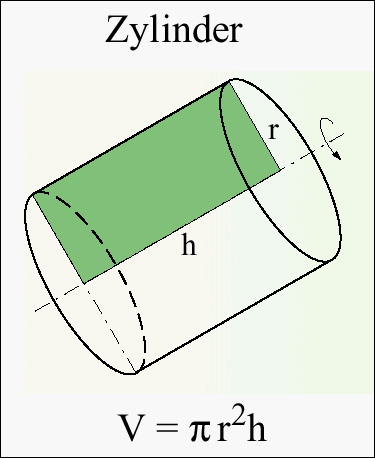
Bestimmung des Zylindervolumens mit der Volumenformel
Aufgabe 8.1: Mit der Volumenformel soll das Volumen eines
Zylinders mit Radius r = 2cm und der Höhe a) Stellen Sie die Funktionsgleichung der Funktion
f auf, deren Graph bei Rotation um die b) Berechnen Sie nun mit Hilfe der Volumenformel das Zylindervolumen. Aufgabe 8.2: Bestimmen Sie das Volumen des Zylinders mit Radius r > 0 und der Höhe h > 0. Stellen Sie hierzu zunächst die Funktionsgleichung der Funktion f auf, deren Graph bei Rotation um die x-Achse den beschriebenen Zylinder im Intervall [ 0 ; h ] erzeugt.
|
|
|
|
|